Quiz 2

NAME: ANSWER KEY

Question 1: Compositions of Isometries (short answer)

Answer with one ore more names indicating all the possible kinds of isometry that are possible consistent with the given information.

a) If S is a glide reflection and T is a line reflection, then ST can be a

Rotation or a translation (identity and halfturn also correct but not required)

b) If U is a translation and V is a glide reflection, then VU can be a

Line reflection or glide reflection.

c) Suppose point A is on line m. Then if M is line reflection in line m and N is point reflection in point A, MN can be a

Line reflection. Not glide reflection in general. Only glide reflection possible has glide vector zero, i. e., line reflection.

Reason: if this is written as a triple line reflection all the mirror lines are concurrent at A.

d) If E is a translation and F is a point reflection, EF can be a

Point reflection (half turn). Not rotation in general. Only rotation possible is with 180 degree angle.

Question 2: State a theorem.

Write down clearly and correctly the statement of one of the 3 fundamental theorems of isometries (hint: the number 3 figures prominently in two of the theorems).

See Brown, Section 1.10, The Fundamental Theorems of Isometries.

Question 3: Answer in complete sentences.

a) What is the definition of an isometry of the plane?

Answer: An isometry of the plane is a transformation of the plane that preserves distance.

Reference: Brown, 1.2, 1.4.

Comment: In general, an isometry is a transformation that preserves distance. A transformation is a one-to-one and onto mapping of a set that is its domain and range. The domain is part of the definition of the transformation. So a transformation of the plane is a one-to-one and onto mapping of the entire plane. Other transformations studied in geometry include transformations of 3-space or the transformations of a sphere. Thus an isometry of 3-space (which we have not studied this quarter) is a transformation of 3-space that preserves distance. An isometry of a sphere is a transformation of a sphere that preserves distance.

b) If T is an isometry of the plane and ABC is a triangle, why is the image of ABC by T a triangle congruent to ABC?

Answer: These distances are equal by the definition of isometry:

T(A)T(B) = AB; T(B)T(C) = BC; T(C)T(A) = CA.

Therefore triangle T(A)T(B)T(C) is congruent to triangle ABC by SSS.

Reference: Brown, 1.6, Theorem 3.

c) If F is a figure in the plane, what is the definition of a symmetry of F?

Answer: A symmetry of a figure is any isometry that maps the figure into itself.

Reference: Brown, 1.9.

d) If A and B are two symmetries of F, why is AB also a symmetry of F (if it must be)?

Answer: If A is a symmetry of F, by the definition A(F) = F. Likewise B(F) = F. To see that AB is a symmetry, consider the image of F: AB(F) = A(B(F)) = A(F) = F, so AB is a symmetry.

Comment: This statement is the key to proving that the symmetries of F form a transformation group (Brown, 2.5, 2.6). This is how the group property is proved. It is not correct to state prove (d) by stating that the symmetries are a group because the group is proved by proving proposition (d) and also proving that the inverse of A is a symmetry. Likewise, you can't prove that a line reflection preserves distance because is it an isometry. It is an isometry because you can prove it preserves distance.

Question 4: (Short answer)

In the figure below, all the chords have equal length. Recall that the notation for rotation with center Z by angle a is Za.

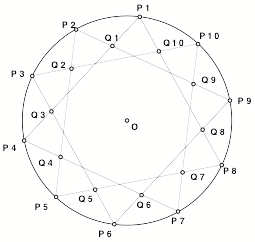
Answer each of these questions. You do not have to give reasons for your answers.

a) How many rotational symmetries does this figure have (including the identity)?

Answer: 10

Comment: The rotations A_t, where t = k*36 degrees, k = 0, 1, 2, …, 9.

b) How many line reflection symmetries does this figure have? ______________

Answer: 10

Comment: The line reflections all the lines OP_k and OQ_k. The number of line reflections always equals the number of rotations, if these are finite numbers.

c) What is the measure of angle Q9OP1? ___________________________

Answer: -(36 + 18) = -54 degrees

d) If L1 is line reflection in line OP1 and M9 is line reflection in line OQ9, tell precisely what isometry is the product M9L1. (State defining data or use clear notation.)

Answer: The isometry is O_-108, rotation with center O and angle 2*(-54) degrees. This is also the rotation by 360 – 108 = + 252 degrees.

Comment: Notice that this is one of the rotations in (a). -108 = -3*36 and 252 = 7*36.

e) Continuing with L1 and M9 and with L5 = line reflection in OP5, tell precisely what isometry is the product L1L5M9. (State defining data or use clear notation.)

Answer: M₁₀ = Line reflection in OQ₁₀. Since line OQ₁₀ = line OQ₅, this could also be denoted as the reflection M₅ in OQ₅.

Comment:

Solution method 1 (use theorem and check image of one point): By Brown, p. 53 #18 this must be a line reflection. So knowing this, one only needs to track one point E to image E' and take perpendicular bisector. For example L1L5M9 (Q₉) = L1L5 (Q₉) = L1 (Q₁₀) = Q₁. The line OQ₁₀ is the perpendicular bisector of Q₉Q₁.

Solution method 2 (use double reflection equality): Use the method of proof of Brown, p. 53 #18 to get equality of two rotations (double reflections). Use angle equality P₁OP₅ = angle Q₅OQ₉ to see that L1L5 = M5M9 and then by algebra that L1L5M9 = M5. Note that M₅ = M₁₀.

f) Tell as precisely as possible: What isometry is O72M9?

Answer: M₁₀ = Line reflection in OQ₁₀. Since line OQ₁₀ = line OQ₅, this is also the reflection M₅ in OQ₅.

Comment: Since L1L5 = M5M9 = O72, this is the same problem as (e).

Question 5: Construction

Let the rotation S = A₂₄₀ and let T = B₁₈₀. If U = ST, tell what kind of isometry is U and construct its geometric defining data.

Answer: U is the rotation with center C and angle 60 degrees, where C is constructed in the triangle below. Angle ABC = 90 degrees, angle CAB = 60 degrees, angle BCA = 30 degrees.

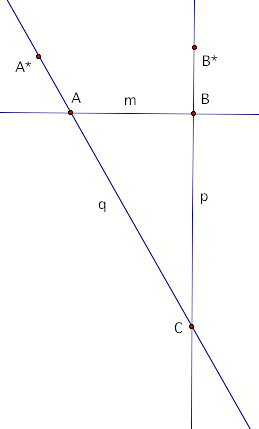
Comment: By the theorem (and details in the proof) of Brown, p. 69, Theorem 23, one knows in advance that U is a rotation by 180 + 240 degrees = 420 degrees, which is a rotation by 60 degrees. Denote by C the center of the rotation U. Then C is the intersection of a line AA* through A and a line BB* through B. One finds these lines by factoring each of the rotations S and T into a double line reflection.

In particular, let m = line AB = line BA.

• Then T = R_m R_q, where p = line BB*, so that angle B*BA = 90 degrees, since 90 = 180/2..
• S = R_qR_m, where q = line AA*, so that angle BAA* = 120 degrees, since 120=240/2.

Then U = ST = R_qR_m R_m R_q = R_q R_q .

Construct the figure with the lines as above. Since 90 + 120 > 180, the angles B*BA and BAA* are exterior angles of the triangle BAC.

C , the intersection of the two lines p and q is the center of the rotation U = C₆₀. Notice that angle BCA = 30 degrees, which is 60/2, as it should be.